9. Recursivitate
2019/03/21 in Programare in C
Spunem despre o functie ca este recursiva daca ea se autoapeleaza. Ea se poate autoapela fie direct, fie indirect prin apelul altor functii.
In limbajele C si C++ se pot defini functii recursive fara a fi nevoie de a specifica acest lucru.
La apelurile recursive ale unei functii aceasta este reapelata inainte de a se reveni din ea. La fiecare reapel al functiei, parametrii si variabilele automatice ale ei se aloca pe stiva intr-o zona independenta. De aceea, aceste date au valori distincte la fiecare reapelare. Nu acelasi lucru se intampla cu variabilele statice. Ele ocupa tot timpul aceeasi zona de memorie si deci ele pastreaza valoarea la un reapel.
Orice apel al unei functii conduce la o revenire din functia respectiva la punctul urmator celui din care s-a facut apelul.
Trebuie amintit ca la revenirea dintr-o functie se procedeaza la curatirea stivei, adica stiva se reface la starea din-aintea apelului. De aceea, orice reapel al unui apel recursiv va conduce si el la curatirea stivei, la o revenire din functie si deci parametrii si variabilele locale vor reveni la valorile lor din-aintea apelului respectiv. Numai variabilele statice raman neafectate de o astfel de revenire.
Functiile recursive se utilizeaza la definirea proceselor recursive de calcul.
Un proces de calcul se spune ca este recursiv, daca el are o parte care se defineste prin el insusi. Un exemplu simplu de astfel de functie este functia de calcul al factorialului. Intr-adevar functia fact(n) de calcul al factorialului se poate defini astfel:
fact(n) = 1, daca n = 0;
altfel
fact(n) = n*fact(n-1)Alternativa fact(n) = n*fact(n-1) defineste functia fact(n) prin ea insasi.
Un proces recursiv trebuie totdeauna sa contina o parte care nu se defineste prin el insusi.
In exemplul de sus, alternativa fact(n) = 1, daca n = 0 este partea care este definita direct.
Definitia de mai sus se transcrie in C astfel:
double fact(int n) /* calculeaza n! */
{
if(n == 0)
return 1.0;
else
return n*fact(n-1);
}
Sa urmarim executia acestei functii pentru n = 3.
La apelul din functia principala se construieste o zona pe stiva in care se pastreaza adresa de revenire in functia principala, dupa apel, precum si valoarea lui n, ca in figura de mai jos:

Deoarece n > 0, se executa alternativa else. Aceasta contine expresia (1) n*fact(n-1)
care autoapeleaza (direct) functia fact. Reapelarea functiei se realizeaza cu valoarea n-1 = 3-1 = 2.
Prin aceasta se construieste o zona noua pe stiva, care contine revenirea la evaluarea expresiei de mai sus, precum si valoarea noua a
parametrului n, adica valoarea 2. Se obtine starea din figura de mai jos.

La noua reapelare a functiei fact, n=2 > 0, deci din nou se executa alternativa else.
Evaluarea expresiei (1) conduce la o reapelare cu valoarea n-1 = 2-1 = 1. Se obtine configuratia:
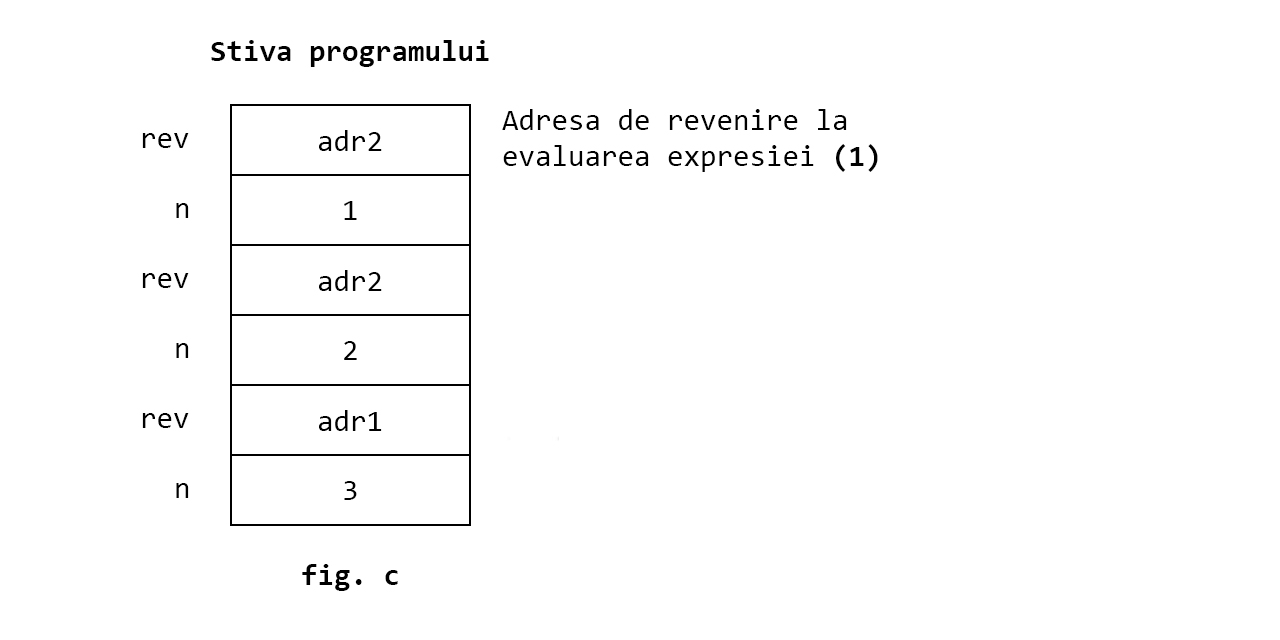
Din nou n=1 > 0 si deci se face o noua reapelare si se obtine configuratia:

In acest moment n=0, deci se revine din functie cu valoarea 1.
Se curata stiva si se revine la configuratia din fig. c.
Adresa de revenire permite continuarea evaluarii expresiei (1).
In acest moment n are valoarea 1 si cum s-a revenit tot cu valoarea 1, se realizeaza produsul
1*1 = 1Dupa evaluarea expresiei (1) se realizeaza o noua revenire tot cu valoarea 1. Dupa curatirea stivei se ajunge la configuratia din fig. b. In acest moment, n are valoarea 2. Evaluand expresia (1), se realizeaza produsul:
2*1 = 2Apoi se revine din nou din functie cu valoarea 2. Dupa curatirea stivei se ajunge la cofiguratia din fig. a.
In acest moment n are valoarea 3. Se evalueza expresia (1) si se obtine:
3*2 = 6Se revine din functie cu valoarea 6 (adica 3!), conform adresei de revenire din functia principala din care s-a apelat functia fact.
In general, o functie recursiva se poate realiza si nerecursiv, adica fara sa se autoapeleze. De obicei, recursivitatea nu conduce la economie de memorie si nici la executia mai rapida a programelor. Ea permite insa o descriere mai compacta si mai clara a functiilor care exprima procese de calcul recursiv. Cu toate acestea, exista cazuri cand functiile recursive, desi au exprimari clare, ele nu sunt recomandate deoarece implica consum mare de timp si memorie, in comparatie cu varianta nerecursiva a aceluiasi proces de calcul. De exemplu, algoritmul de generare a permutarilor de n obiecte poate fi descris atat recursiv cat si nerecursiv. O varianta recursiva simpla genereaza permutarile de n obiecte inserand un obiect nou (n) in toate pozitiile posibile in permutarile de n - 1 obiecte. Acest algoritm, desi este mai simplu decat varianta nerecursiva, el nu este practic, deoarece generarea permutarilor de n obiecte presupune existenta deja in memorie a permutarilor de n - 1 obiecte, ori n! creste foarte rapid, ceea ce conduce la un necesar mare de memorie chiar si pentru un n mic. Se pot indica si alte functii recursive ineficiente fata de variantele lor nerecursive. De exemplu, in multe lucrari se prezinta functia recursiva pentru calculul numerelor lui Fibonacci si se arata ineficienta ei fata de varianta nerecursiva.
De aceea, rezolvarile cu ajutorul functiilor recursive urmeaza sa se adopte numai dupa un studiu atent al implicatiilor pe care le au acestea in privinta necesarului de memorie si al timpului de executie.
Exista cateva tipuri de probleme care, de obicei, se rezolva cu ajutorul functiilor recursive. Astfel, se recomanda sa se utilizeze functii recursive pentru probleme a caror metode de rezolvare pot fi definite recursiv.
In aceasta clasa se includ metode de divizare, metode de cautare cu revenire (backtracking) etc.
In toate cazurile trebuie insa sa se aiba in vedere necesarul de memorie si al timpului de executie in comparatie cu variantele nerecursive.
Exercitii:
9.1. Sa se scrie un program care citeste pe n de tip int, calculeaza si afiseaza n! folosind functia recursiva fact definita mai sus.
- Programul 109 - Factorial cu functie recursiva
#include <stdio.h>
#include <stdlib.h>
#define MAX 170
double fact(int n) /* calculeaza n! */
{
if(n == 0)
return 1.0;
else
return n*fact(n-1);
}
main()
{
int n;
char t[255];
for( ; ; ) {
printf("valoarea lui n: ");
if(gets(t) == 0) {
printf("s-a tastat EOF\n");
exit(1);
}
if(sscanf(t, "%d", &n) == 1 && n >= 0 && n <= MAX)
break;
printf("se cere un intreg din intervalul [0, %d]\n", MAX);
}
printf("n = %d\tn! = %g\n", n, fact(n));
}
9.2. Sa se scrie o functie recursiva care calculeaza numarul aranjamentelor de n obiecte luate cate k,
pentru n >= k > 0.
Daca notam cu A(n,k) numarul aranjamentelor de n obiecte luate cate k, atunci:
A(n,k) = n(n-1)(n-2)...(n-k+1) =
= n(n-1)(n-2)...((n-1)-(k-1)+1) =
= nA(n-1,k-1)
A(n,1) = nRelatia de mai sus, pentru calculul numarului aranjamentelor, este recursiva. Ea se transcrie in limbajul C folosind o functie recursiva.
- FUNCTIA110.C - Aranjamente de n cate k cu functie recursiva
double aranjamente(n, k)
/* returneaza numarul aranjamentelor de n obiecte luate cate k /
unde n >= k > 0 */
{
if( k == 1 )
return (double) n;
else
return n*aranjamente(n-1, k-1);
}
9.3. Sa se scrie un program care citeste doi intregi n si k,
1 <= n <= 170
1 <= k <= nValorile lui n si k se citesc folosind functia pcit_int_lim definita in exercitiul 8.3. Aceasta functie, la randul ei, apeleaza functia pcit_int definita in exercitiul 8.2.
- Programul 110 - Aranjamente n cate k cu functie recursiva
#include <stdio.h>
#include <stdlib.h>
#include "FUNCTIA094B.C";
#include "FUNCTIA094C.C";
#include "FUNCTIA110.C";
#define MAX 170
main()
{
int n, k;
char er[] = "S-a tastat EOF\n";
if(pcit_int_lim("n = ", 1, 170, &n) == 0) {
printf(er);
exit(1);
}
if(pcit_int_lim("k = ", 1, 170, &k) == 0) {
printf(er);
exit(1);
}
printf("n = %d\tk = %d\tA(n, k) = %g\n", n, k, aranjamente (n, k));
}
9.4. Sa se scrie o functie care are ca parametri doi intregi m si n de tip long si care calculeaza si returneaza cel mai mare divizor comun al lor.
Notam cu (m,n) cel mai mare divizor comun al numerelor m si n.
Calculul celui mai mare divizor comun a doua numere se poate realiza recursiv astfel:
| (m,n) = m | daca n = 0; |
| (m,n) = n | daca m = 0; |
| (m,n) = (n,m%n) | daca atat m cat si n sunt diferiti de zero si m > n
(prin m%n s-a notat restul impartirii lui m la n) |
- FUNCTIA111.C - cmmdc cu functie recursiva
long cmmdc(m, n)
{
if( m == 0 )
return n;
else
if( n == 0 )
return m;
else
if( m > n)
return cmmdc(n, m%n);
else
return cmmdc(m, n%m);
}
9.5. Sa se scrie un program care citeste doi intregi pozitivi m si n, de tip long, calculeaza si afiseaza cel mai mare divizor comun al lor.
- Programul 111 - Cmmdc cu functie recursiva
#include <stdio.h>
#include <stdlib.h>
#include "FUNCTIA111.C";
main()
{
long m, n;
printf("valorile lui m si n: ");
if(scanf("%ld %ld", &m, &n) != 2 || m < 0 || n < 0) {
printf("nu s-au tastat doi intregi pozitivi\n");
exit(1);
}
printf("m = %ld\tn = %ld\t(m,n) = %ld", m, n, cmmdc(m,n));
}
9.6. Sa se scrie un program pentru rezolvarea problemei Turnurilor din Hanoi. Aceasta problema se enunta ca mai jos:
Se considera trei tije, A, B si C si n discuri de diametre diferite. Tijele sunt fixate vertical pe o placa. Discurile au fiecare cate un orificiu in centru si ele pot fi aranjate pe fiecare din cele trei tije. Initial toate discurile sunt puse pe tija A si ordonate in asa fel incat orice disc este asezat peste un disc de diametru mai mare decat al lui. Daca numerotam discurile in ordinea crescatoare a diametrelor lor, adica discul 1 are diametrul cel mai mic, apoi discul 2 are diametrul urmator si asa mai departe, discul n avand diametrul cel mai mare, atunci discul 1 se afla in varf, sub el discul 2 etc., iar la baza se afla discul n.
Se cere sa se mute discurile de pe tija A pe tija B, folosind tija C ca tija de manevra. La fiecare mutare se muta un singur disc si anume, unul aflat in varful discurilor de pe alta tija se pune in varful discurilor de pe o alta tija sau pe placa daca tija respectiva nu contine discuri. De asemenea, nu se poate muta un disc de diametru mai mare peste unul de diametru mai mic. Deci, la o mutare, peste discul k se poate aseza numai unul din discurile 1, 2, ..., k-1. In final, discurile trebuie sa fie asezate pe tija B in aceeasi ordine in care s-au aflat pe tija A, adica in varf sa fie discul 1, sub el discul 2 si asa mai departe, discul n aflandu-se la baza.
Problema Turnurilor din Hanoi pentru n discuri se rezolva imediat daca stim sa o rezolvam pentru n-1 discuri. Intr-adevar, in ipoteza ca stim sa rezolvam problema pentru n-1 discuri, procedam astfel:
- se deplaseaza discurile 1, 2, ..., n-1 de pe tija A pe tija C
- discul n se muta de pe tija A pe tija B;
- cele n-1 discuri de pe tija C se deplaseaza pe tija B.
In felul acesta, pe tija B se afla toate cele n discuri si in ordinea ceruta, adica 1, 2, ..., n.
Deci rezolvarea problemei turnurilor din Hanoi cu n discuri s-a redus la rezolvarea aceleiasi probleme, dar cu n-1 discuri.
In mod analog, problema pentru n-1 discuri se poate rezolva daca stim sa o rezolvam pentru n-2 discuri.
In felul acesta, din aproape in aproape, ajungem la concluzia ca problema Turnurilor din Hanoi pentru n discuri se poate rezolva,
daca stim sa o rezolvam pentru n = 1. Ori in acest caz problema este rezolvata imediat: se muta discul de pe tija pe care se afla
(tija sursa), pe tija pe care dorim sa se afle discul (tija destinatie).
Cele trei tije se afla in una din urmatoarele stari posibile:
| tija sursa | cotine discurile care trebuiesc transferate pe alta tija; |
| tija destinatie | tija pe care trebuie sa se afle discurile transferate de pe tija sursa; |
| tija de manevra | tija care se foloseste pentru a stoca temporar discuri. |
Rolul tijelor se schimba in diferite etape ale procesului de deplasare a discurilor si de aceea, rolul fiecarei tije se defineste cu ajutorul parametrilor.
Mai jos definim o functie recursiva pe care o numim hanoi. Ea are 4 parametri:
| n | numarul discurilor; |
| a | tija sursa |
| b | tija destinatie |
| c | tija de manevra |
Apelul hanoi(n, 'A', 'B', 'C'); inseamna ca se rezolva problema pentru n discuri.
Acestea se afla pe tija A, tija B este tija destinatie, iar tija C este tija de manevra.
Functia hanoi afiseaza fiecare mutare, indicand numarul discului, tija de pe care se muta discul respectiv, precum si tija pe care se muta el.
Dupa afisarea unei mutari, se apeleaza functia getch pentru a bloca executia programului. In felul acesta se poate analiza mutarea afisata de calculator.
Trebuie mentionat ca problema de fata poate fi rezolvata si nerecursiv. Varianta nerecursiva este mai complexa decat cea recursiva.
- Programul 112 - Turnurile din Hanoi
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
void hanoi(int n, int a, int b, int c)
/* functie recursiva pentru rezolvarea
problemei turnurilor din Hanoi
n - numarul discurilor;
a - tija sursa;
b - tija destinatie;
c - tija de manevra. */
{
if(n == 1) { /* n = 1 */
printf("se muta discul 1 de pe tija: %c pe tija: %c\n", a, b);
getch();
return;
}
/* n > 1;
se rezolva problema pentru n-1 discuri;
a - tija sursa;
c - tija destinatie;
b - tija de manevra. */
hanoi(n-1, a, c, b);
/* discul n de pe tija a se muta pe tija b */
printf("discul %d de pe tija: %c se muta pe tija: %c\n", n, a, b);
getch;
/* n > 1;
se rezolva problema pentru n-1 discuri;
c - tija sursa;
b - tija destinatie;
a - tija de manevra. */
hanoi(n-1, c, b, a);
}
/* sfarsit hanoi */
main()
/* citeste pe n si rezolva
problema Turnurilor din Hanoi
pentru n discuri */
{
int n;
char t[255];
for( ; ; ) {
printf("numarul discurilor = ");
if(gets(t) == 0) {
printf("s-a tastat EOF\n");
exit(1);
}
if(sscanf(t, "%d", &n) == 1 && n > 0)
break;
printf("nu s-a tastat un intreg pozitiv\n");
}
hanoi(n, 'A', 'B', 'C');
}
 Link.RO
Link.RO